
Publications
An overview of my research
This is a layperson summary of the type of research I do, for more technical details please see my papers below.
If I was to ask you for a complete physical description of water, it’s quite likely your mind would immediately jump to the liquid phase of water, like the type in your water bottle now. Water as a liquid can be thought of as layers of molecules of H20 which slide past each other. You know water in other phases too; ice and steam. Ice is the solid phase of water and may be thought of as the same H20 molecules arranged in a lattice. Steam is the gaseous phase of water and it may be thought of as individual molecules of water which bounce around and collide with each other (with some small interactions).
The question of a complete physical description of water is a challenging one, since although water is still just molecules of H20, their behaviour can be vastly different depending on what phase it is in! A useful physical characterisation of water is to identify its phases and how to transition between them. You already know how to do these phase transitions in your everyday life, for example you could heat up ice which melts into liquid water and then boils to steam. You could also increase the pressure which would compress the molecules bringing them closer on average i.e. going from steam to liquid to solid. One thing that summarises the phases of water is the phase diagram, tells you the phase that water is in at a given temperature and pressure. Here’s a picture below (from Siemens Stiftung Media Portal):
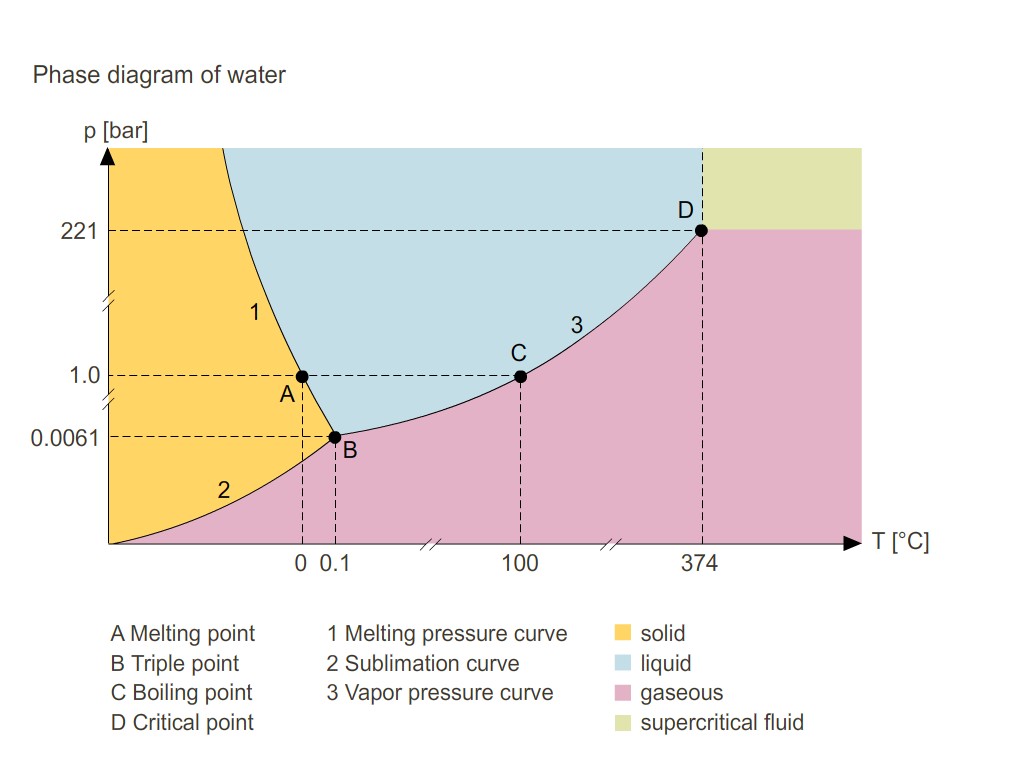
My research is about understanding the phase diagrams of certain supersymmetric particle models. Just like how molecules of H20 were the building blocks of the phases of water, certain particles called quarks and monopoles are the building blocks for the models I study. The different phases of a supersymmetric particle model refers to the types of composite objects the quarks and the monopoles can form and what symmetries they enjoy. These phases can be summarised in a phase diagram like above.
- S. Bennett, A. Hanany and G. Kumaran, “Orthosymplectic quotient quiver subtraction II: Framed Quivers,” arXiv, 2025.
Summary: We continue the program of finding combinatorial techniques to explore hyper-Kähler quotients on symplectic singularities on supersymmetric gauge theories. Our previous work did this for so called “orthosymplectic quiver gauge theories” we complete the analysis for another type of orthosymplectic quiver with a property called “framing”.
- S. Bennett, A. Hanany, G. Kumaran, C. Li, D. Liu and M. Sperling, “Quiver subtraction on the Higgs branch,” Nuclear Physics B, vol. 1016, p. 116917, 2025.
Summary: We turn the Higgs mechanism of certain supersymmetric gauge theories into a combinatorial technique. Using this we are able to understand the different phases of these theories.
- S. Bennett, A. Hanany and G. Kumaran, “Orthosymplectic quotient quiver subtraction,” Journal of High Energy Physics, vol. 12, p. 063, 2024.
Journal of High Energy Physics · Dec 10, 2024
Summary: Taking inspiration from six dimensional physics we develop another diagrammatic technique on quiver gauge theories which correspond to hyper-Kähler quotients on symplectic singularities. One application is to find a perturbative (Lagrangian) realisation of the physics of certain strongly interacting objects in string theory called M5 branes. This was not thought possible before.
- A. Hanany, R. Kalveks and G. Kumaran, “Quiver polymerisation,” Journal of High Energy Physics, vol. 11, p. 168, 2024.
Journal of High Energy Physics · Nov 28, 2024
Summary: We continue to explore hyper-Kähler quotients on symplectic singularities which have realisations combinatorially on supersymmetric gauge theories, which can be expressed diagrammatically. This combinatoric action “polymerises” these diagrams either gluing them together or by introducing a loop.
- A. Hanany, G. Kumaran, C. Li, D. Liu and M. Sperling, “Actions on the quiver: discrete quotients on the Coulomb branch,” Journal of High Energy Physics, vol. 05, p. 318, 2024.
Journal of High Energy Physics · May 29, 2024
Summary: We explore discrete group actions on a class of geometric objects called symplectic singularities. These discrete group actions have simple realisations in a combinatoric way on certain supersymmetric gauge theories called quiver gauge theories.
- A. Hanany, R. Kalveks and G. Kumaran, “Quotient quiver subtraction,” Nuclear Physics B, vol. 1009, p. 116731, 2024.
Summary: We give a combinatoric prescription to understand a certain geometric operation called a hyper-Kähler quotient on a class of geometric objects called symplectic singularities. This combinatoric prescription has origins in certain supersymmetric gauge theories called quiver gauge theories. Dissertat
Project
MSc Quantum Fields and Fundamental Forces, Imperial College London, dissertation, September 2022.